Many of you have certainly heard about the TSP problem (Travelling Salesman Problem).
His target is to find the shortest tour that visits every city (just once) and return to the start city...

From xkcd.com ( http://xkcd.com/399/ )

For the algorithm class we had the excercise ("Algorithm Cup") to try out the best solution we could find on 10 TSP problems (from the TSPLIB). We have some restriction too, the algorithm has to run on a "simple machine" (duo-core) and has a time limit of 3 minutes for each instance (for each problem).

Considering I've not much time, I choose this approach for implementing my solution:
1) Construction algorithm: Nearest Neighbour 
2) Local optimization: 2/2.5 - OPT (web simulation applet)
3) Meta-Heuristics: Simulated Annealing

My expectation (error from the optimal solution) for the above algorithms (depending on the problem):
1) Around 21-26 %
2) Around 4-8%
3) Lower than 1%

Let's start coding (in C), as data structure I choose the simplest (and fastest) possible: array of integer.
First we need to parse the TSPLIB problem files (.tsp) and construct our distances[][] array, my decision was to keep exactly the same numbering of cities from the problem as index of all my arrays.

For example distances[1][2] give me the distance from city one to city two.

I keep my actual tour in an array named tour[] and I used to pass this to my functions where I've implemented the algorithms.

Construction Algorithm: Nearest Neighbour
// Compute Nearest Neighbour
// Return running time in ms
double nearestNeighbour(int *_cityPath)
{
 clock_t start, end;
 
 if(DEBUG)
  printf("Nearest Neighbour construction...\n");

 // Start clock
 start = clock();

 // Allocate an "already visited" array (the +1 is cause I start my array from index 1)
 bool *visited = (bool *) calloc(sizeof(bool), dimension+1);
 // Start from city one
 int cityVisited = 1;
 
 int minPath = INT_MAX;
 int *cityPath = _cityPath;
 int ii = 1;
 int j;
 int minPathCity = 0;
 
 // Iterate all cities 
 while(cityVisited <= dimension)
 {
  if(DEBUG)
   printf("Searching neighbor of %d [total: %3d]\n", ii, cityVisited);
  // Iterate through all cites near ii
  for(j=1; j<=dimension;j++)
  {
   // if distance from city ii to j is lower then the minPath 
   if(distances[ii][j] < minPath)
   {
    // if I've not already choose the city
    if(!visited[j])
    {
     // replace the minPath
     minPath = distances[ii][j];
     minPathCity = j;
     //printf("New neighbor for %3d: %3d\n", ii, j);
    }
   }
  }
  // set 
  cityPath[cityVisited] = ii;
  // set ii as already visited
  visited[ii] = true;
  // ii is the next city
  ii = minPathCity;
  // reset minPath to INT_MAX for the next round
  minPath = INT_MAX;
  // increment cityVisited counter
  cityVisited++;
 }
 // Add retour to the first city
 cityPath[cityVisited] = cityPath[1];

 // Compute running time of NN algorithm
 end = clock();
 double ct =((end-start)/ ((double)CLOCKS_PER_SEC)) * 1000.0;
 return ct;
}

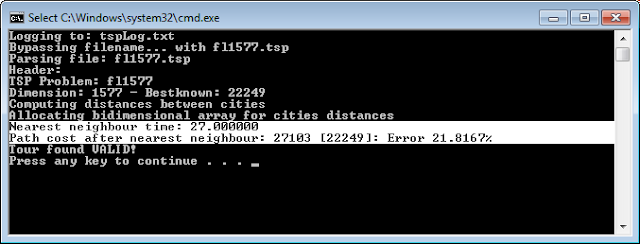
Now let's see how it work on a 1577 cities TSP problem (fl1577.tsp)


In the part two we will se how local optimization can improve this tour...

Keep tuned!